(🏠 elijahcaine.me) (🐙 github 🐱) (👔 resume) (📰 feed)

Elliptic Curve Cryptography

Wed 04 October 2017

Note

This is a part of a series of blog posts I wrote for an Independent Study on cryptography at Oregon State University. To read all of the posts, check out the 'Independent Crypto' tag.

Warning

This post is jumps around a bit. We'll start by showing how Elliptic Curve Cryptography works at a high level, then create a list of questions about how/why Elliptic Curve Cryptography works and how it is useful to cryptogrpahy. Once those questions are answered we will end with a recap. Hopefully we will zero in on what Elliptic Curves are and what Elliptic Curve Cryptography is.

Diffie-Hellman key exchange ++

You find yourself day-dreaming during a walk around campus wondering if there is an alternative cryptography system to the very popular RSA. You want something that has improved computational and network efficiency. You want smaller keys that are harder to crack. Could such a system exist?

You share this fantasy with a friend, you share all of your crypto fantasies with this friend, and they tell you that Elliptic Curve Cryptography is promising and it perfectly fits your needs. ... but how does it work?

Diffie-Hellman key exchange (a recap)

To create a useful crypto out of Elliptic Curves we need to implement Diffie–Hellman key exchange (DHKE). Once we have DHKE we more or less have a valid crypto system which we can build upon to encrypt and decrypt private information.

The reader (you) is assumed to be familiar with DHKE. While DHKE is fairly simple, it is not unforgettable, so here is quick reminder:

  1. Alice and Bob agree on a public modulus (p) and a base (g).
  2. Alice and Bob both choose secret integers (a and b).
  3. Alice sends Bob ga (mod p) (we call it A) and Bob sends Alice gb (mod p) (we call it B).
  4. Alice computes Ba (mod p) and Bob computes Ab (mod p). These are equivalent (mod p). This is Alice and Bob's shared secret.

How do we use Elliptic Curves get a similar 'shared secret'?

Elliptic Diffie-Hellman key exchange

At a (very) high level the algorithm is as follows:

  1. Alice and Bob agree to use a given Elliptic Curve over a finite field, E(Fp), and a public point P ∈ E(Fp).
  2. Alice chooses a secret integer nA and Bob choose secret integers nB.
  3. Alice computes QA = nAP and Bob computes QB = nBP. These are the "Public Keys"
  4. Alice sends Bob her public key, Bob send Alice his public key.
  5. Alice computes nAQB, Bob computes nBQA.
  6. The shared secret value is nAQB = nA(nBP) = nB(nAP) = nBQA

It looks similar to the given DHKE algorithm, and seems promising, but... how does it work?

Elliptic Curves and Elliptic Curve Cryptography Q&A

To answer that we are going to answer the following:

  • What are Elliptic Curves?
  • What does an Elliptic Curve look like?
  • What does it mean to multiply P by n?
  • What about a finite field?
  • How are the pubic keys used? Why are these a shared secret?
  • Why is Elliptic Curve Cryptography useful?

What are Elliptic Curves?

A Elliptic Curve is the set of solutions to an equation of the form

Y2 = X3 + AX + B

What does an Elliptic Curve look like?

Two examples of Elliptic Curves are as follows:

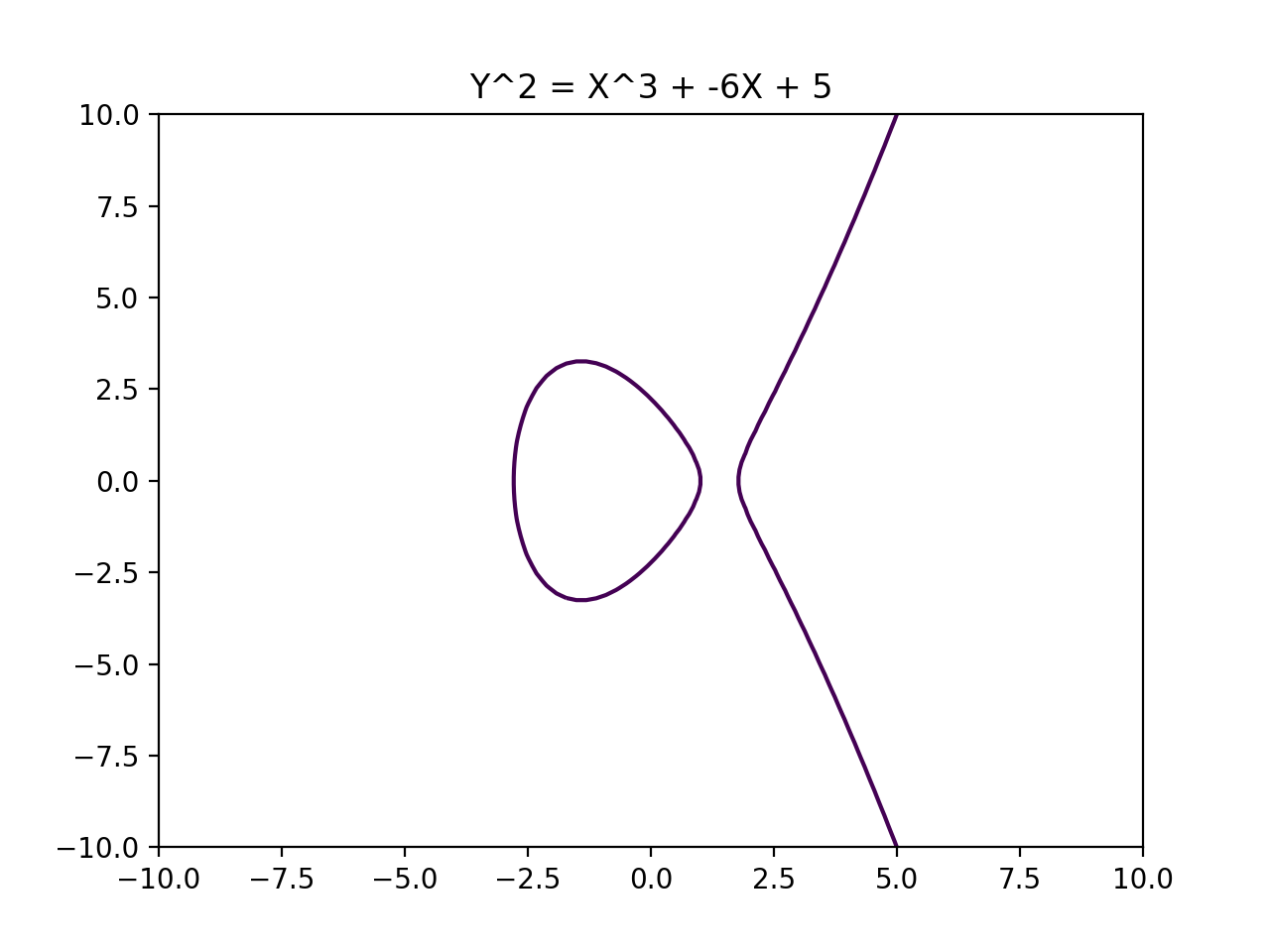
A simple Elliptic Curve

and:

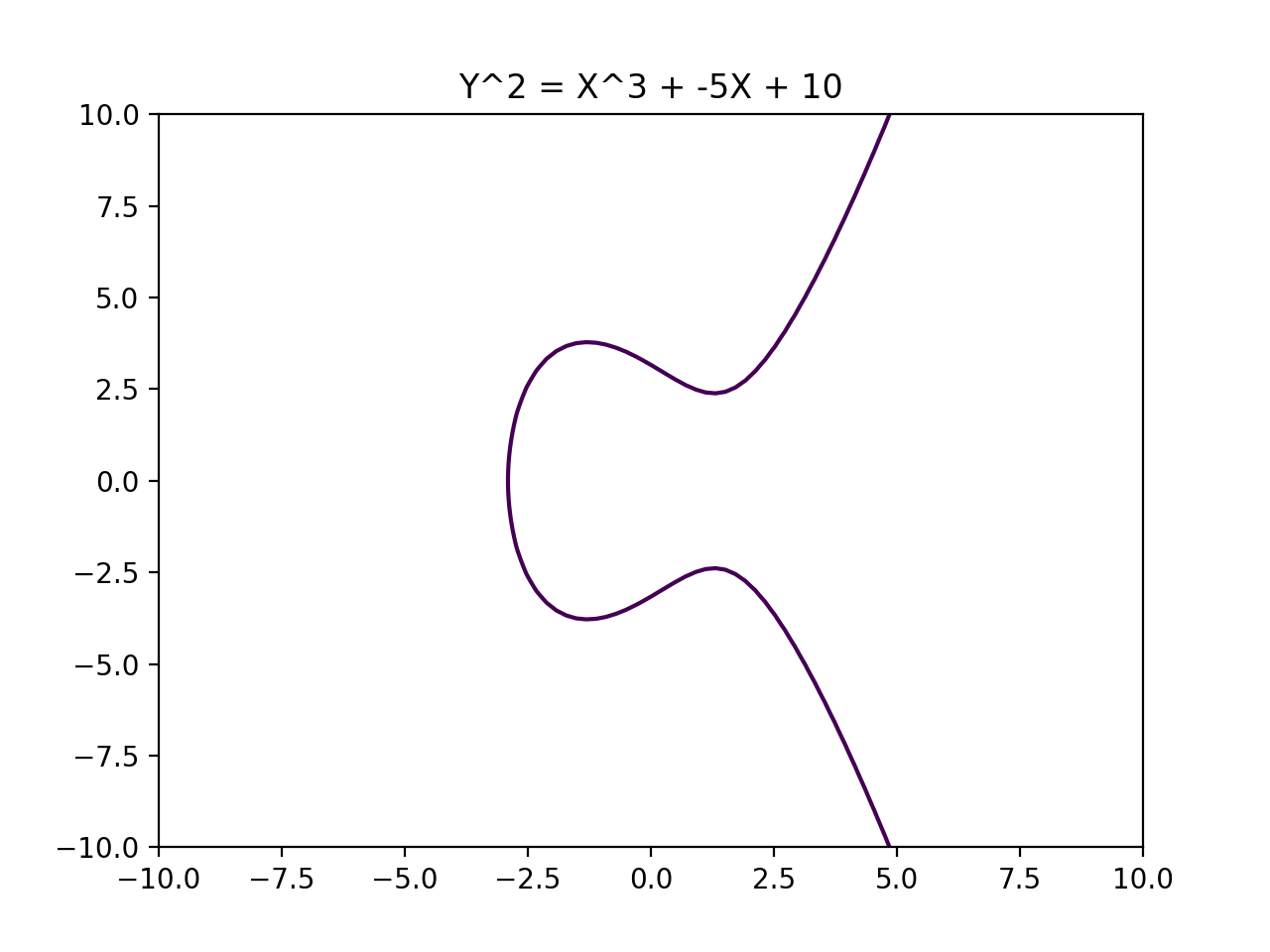
Another simple Elliptic Curve

Adding P and Q

Multiplication is just repeated addition. Oh shoot we haven't said how "addition" happens on an Elliptic Curve. Let's do that.

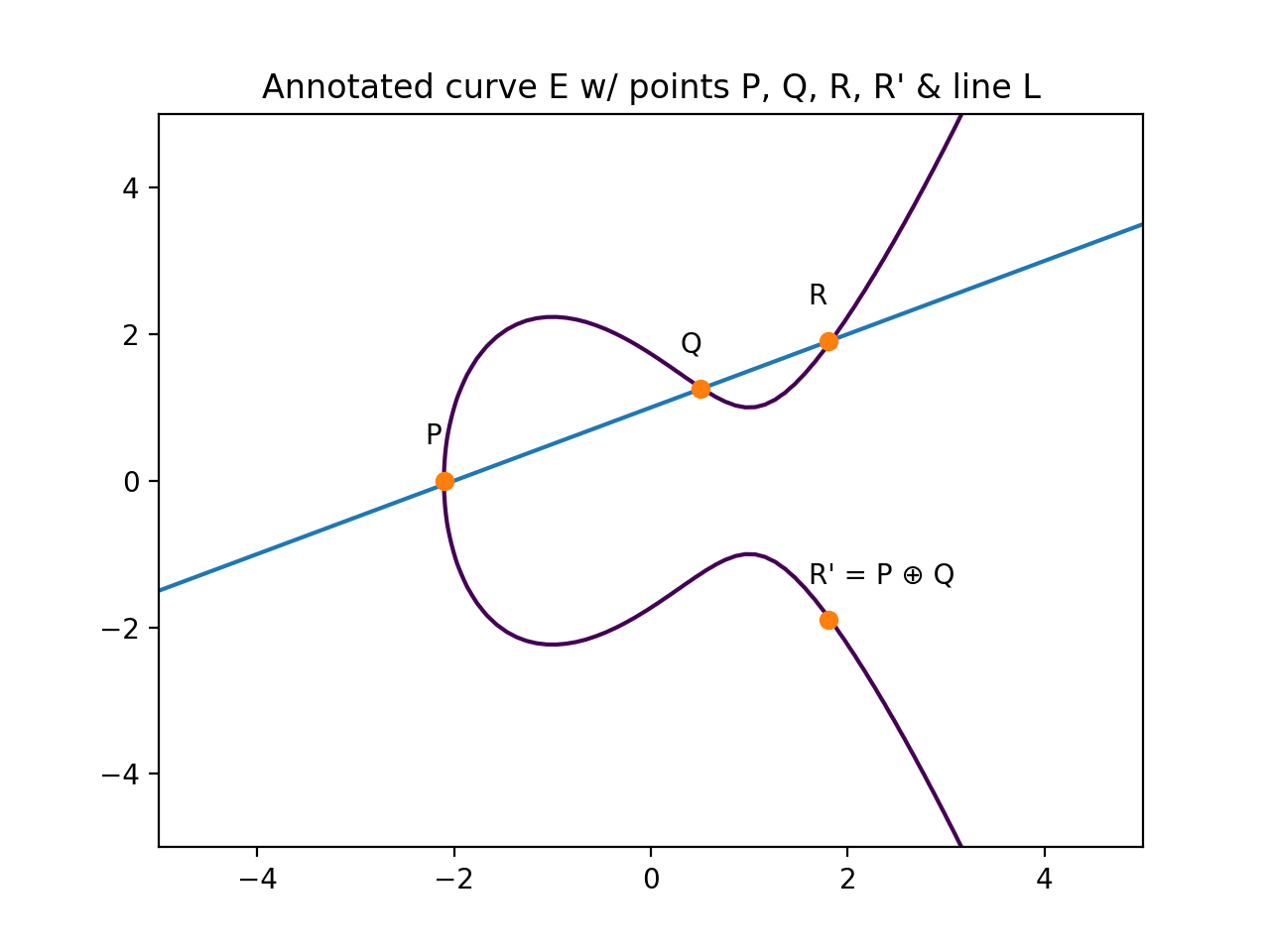
Addition is the process of drawing a line L between P and Q. The third point that the line L intersects is point R. When R is reflected over the X axis we call this R'. The result of P ⊕ Q (read: P 'plus' Q) is R'.

We can enumerate these steps as:

  1. Take two points P and Q on the Elliptic Curve E.
  2. Draw a line L which passes through these two points.
  3. L should ultimately pass through three points: P, Q, and R.
  4. Multiply the Y coordinate of R by -1, this is R'.
  5. P ⊕ Q = R'.

Here's a visualization of straight forward addition.

Annotated curve E with points P, Q, R, R' and line L labeled.

You might think "What happens when P is tangent a point on E?" In that case we say P = Q, so R = P ⊕ P, or R = 2P. It looks like this:

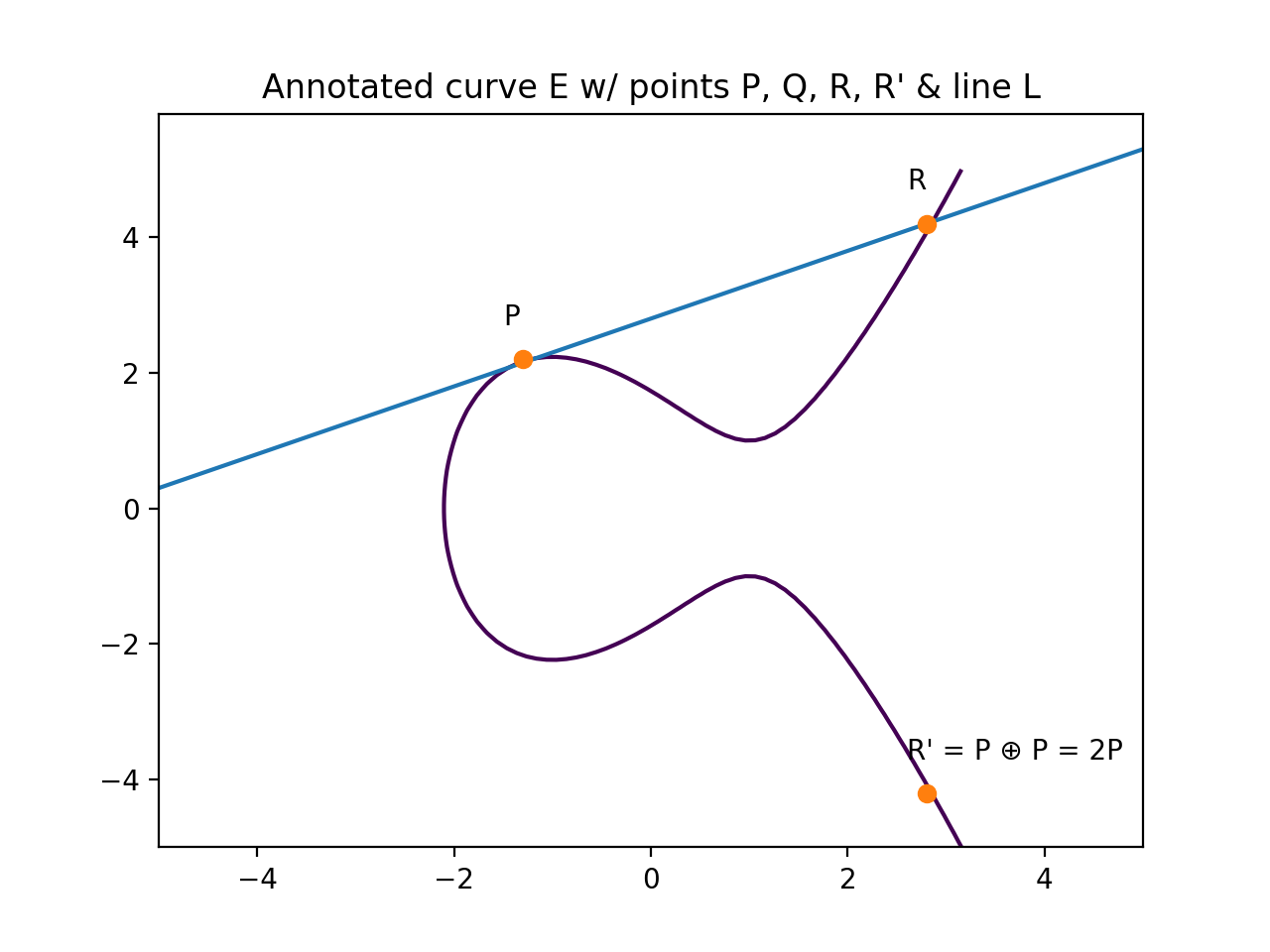
Annotated curve E with points P, R, R' and line L labeled. P is tangent to the curve.

Wait a second, 2P looks like n*P which was one of the questions we had! Don't worry, we'll get there soon.

That thing about Finite Fields

In practice we bound the curve over a field Fp with p ≥ 3. We input {1, 2, ..., p-1} as the value of X in E and select the results which are squares modulo 13.

For example:

E : Y2 = X3 + 3X + 8 over F13
X = 1
1 + 3 + 8 = 12
12 is a square (mod 13)

Repeating this gives us the set of points in E(F13):

E(F13) = {O, (1,5), (1,8), (2,3), (2,10), (9,6), (9,7), (12,2), (12,11)}

In practice this bounds the graph of E and forces us to draw a strange modulus graph shown below:

Elliptic Curves illustrated where each point is a valid coordinate. There are no curves.

Image source: A (relatively easy to understand) primer on elliptic curve cryptography [2]

Multiplying P by an integer with The Double-and-Add Algorithm

To "multiply" P by n we need to use the Double-and-Add Algorithm. Here's how that looks:

  1. Take a point P ∈ E(Fp) and an integer n ≥ 1.
  2. Set Q = P and R = O.
  3. Loop while n > 0.
    1. If n ≡ 1 (mod 2), set R = R + Q
    2. Set Q = 2Q and n = floor(n/2).
  1. Return the point R, which equals nP.

Recall that the algorithm for finding point 2Q was covered in the above section Adding P and Q

What is the shared secret?

Let's review. The shared secret is the second point nAnBP, which is a point on the public curve E(Fp). This point can be used to encrypt information as it is a shared secret (necessary for DHKE). How exactly it is used to encrypt information is left as an exercise for readers in charge of cryptographic implementation standards.

The reason this is a shared secret is because an adversary needs to solve the following Elliptic Curve Discrete Logarithm Problem

nP = QA

Which is a very hard problem, as mentioned in the next section.

An example of Elliptic Curve Cryptography

This sounds good in theory, but let's give it a test drive.

Alice and Bob are given the following shared information:

p = 3851, E: Y2 = X3 + 324X + 1287, P = (920, 303) ∈ E(F3851)

Alice and Bob choose their secret integers:

nA = 1194
nB = 1759

Alice and Bob then compute their public keys:

Alice computes QA = 1194P = (2067, 2178) ∈ E(F3851)
Bob computes QB = 1759P = (3684, 3125) ∈ E(F3851)

Note

Remember that we use the Double-and-Add algorithm to compute QA and QB. This invloves iteratively computing the tangent line at a point, the intersection with E at that intersection, and reflecting that point over the X axis.

Alice and Bob trade public keys and calculate their shared secret:

Alice computes nAQB = 1194(3684, 3125) = (3347, 1242) ∈ E(F3851)
Bob computes nBQA = 1759(2067, 2178) = (3347, 1242) ∈ E(F3851)

Therefore (3347, 1242) is the shared secret.

Why Elliptic Curve Cryptography is useful

While it is harder than simply multiplying mod p for Alice to compute her shared secret (which is the case in RSA), it is even harder for a malicious actor to figure out that same shared secret. This point is best put by the source A (relatively easy to understand) primer on elliptic curve cryptography [2]:

You can compute how much energy is needed to break a cryptographic algorithm and compare that with how much water that energy could boil. This is a kind of a cryptographic carbon footprint. By this measure, breaking a 228-bit RSA key requires less energy than it takes to boil a teaspoon of water. Comparatively, breaking a 228-bit elliptic curve key requires enough energy to boil all the water on earth. For this level of security with RSA, you'd need a key with 2,380 bits.

So an Elliptic Curve Cryptography key can be one magnitude smaller in size and offer the same level of security as RSA.

We can put this in more concrete terms: the fastest algorithm to solve the Elliptic Curve Discrete Logarithm Problem, which Elliptic DHKE security is built upon, in E(Fp) takes √p steps. This is much more difficult than the 'vanilla' Discrete Logarithm Problem.

Notes and edge cases

Elliptic Curve Cryptography, much like the rest of Cryptography, deals heavily with Number Theory. Despite my best efforts most of the nitty-gritty Number Theory in this topic went way over my head. As a result I didn't include much of that kind of stuff and instead focused on the things I could share and sound smart about.

Here are some other things about Elliptic Curve Cryptography I didn't cover that deserve more air time:

  • The Elliptic Curve chosen must meet a special set of criteria; any old Elliptic Curve won't do. This was the cause of a cryptographic breach with Elliptic Curve Cryptography a few years ago that triggered doubts about Elliptic Curve Cryptography as a whole.
  • Some primes cause solving the Elliptic Curve Discrete Logarithm Problem for E(Fp) to be easier than the Discrete Logarithm Problem, these primes can be computed and should be avoided.
  • If you want a deeper understanding of the theory of Elliptic Curves (addition of points on these curves, etc) you should look into algebraic geometry.

Annotated Bibliography

An Introduction to Mathematical Cryptography [1]
The chapter in this textbook on Elliptic Curves in Cryptography established the bedrock understanding of the topic of Elliptic Curve Cryptography. This ended up being the main resource for this post and offered a great median between "Regular Joe's guide to Elliptic Curve Cryptography" and "The graduate student's guide to Elliptic Curve Cryptography" which were my other two resources. It was also the source of all examples, which were very useful in gaining an intuitive understanding of the material.
A (relatively easy to understand) primer on elliptic curve cryptography [2]
This blog post was my second source and did a good job of taking the proofs and dense material in Intro to Math Cyrpto (above) and boiled it down to the important stuff. It drastically improved further readings of the original textbook and provided that great animated image of adding P ⊕ Q in E(Fp). It didn't cover any of the Number Theory, but explained the historical context of Elliptic Curve Cryptography, roughly how/why it works, and did a good job of describing it's impact in our world today.
Cryptography: An Introduction [3]
This wasn't a resource I actually used, but I did read the chapter on Elliptic Curve Cryptography (chapter 2!). It gave me an appreciation for the previous two sources and some exposure to the other ways Elliptic Curves can be taught.

Errata

[1]An Introduction to Mathematical Cryptography, 2008, Jeffery Hoffstein, Jill Pipher, Joseph H. Silverman, Springer Publishing, ISBN 978-0-387-77993-5
[2](1, 2, 3) A (relatively easy to understand) primer on elliptic curve cryptography, October 24, 2013, Nick Sullivan, Cloudflare blog, reposted on Ars Technica, https://arstechnica.com/information-technology/2013/10/a-relatively-easy-to-understand-primer-on-elliptic-curve-cryptography/
[3]Cryptography: An Introduction (Third Edition), May 19, 2016, Nigel Smart, https://www.cs.umd.edu/~waa/414-F11/IntroToCrypto.pdf